Conditional Expectation
- or
- 조건부 기대값
# Tag:
Conditional Expectation(조건부 기대값)
어느 한 값을 알게 된다고 하면, 보통 다른 값에 대해 믿음이 변하는 경우가 많다. 이런 경우는 조건부로 기대값을 구해야 한다.
ex) 아주 큰 값이 나왔다면, 다른 것이 같은 분포일 때 그처럼 비슷한 큰 값이 나올 것이라는 믿음.
- Discrete:
- Continious:
- 조건부 PDF 에 대해서 기대값의 정의로 계산한 결과이다. 베이즈 정리에 의해 맨 오른쪽 식과 동일하게 된다.
위의 경우는 라는 확률 변수 가 특정한 값 라는 조건 하에 의 기대값을 말하는데, 이를 좀 일반화시켜서 말하면 값에 따라 의 기대 값이 달라지는 함수로 볼 수 있다. 즉,
를 이에 대해서 대체해서 쓴다고 하면,
⇒ 즉, 자체에 대한 조건이라고 하면, 값이 달라질 때마다 그에 대한 의 기대 값이 나오는 함수 = 확률 변수가 나오게 된다. 즉, 를 정의역으로 가지는 함수이다.
다시 정리하면,
- 가 조건 ⇒ 특정 값.
- 가 조건 ⇒ 함수.
⇒ 이면 이고, 각 값의 확률은 동일하므로 그를 합치면 0이 된다.
Properties
- ⇒ 를 알고 있으므로 도 알고 있어 상수 취급 가능해 빼낼 수 있음.
- 와 가 독립일 때
- 필요충분조건으로써 성립하지는 않는다. 기대값이 위처럼 나오더라도, 둘은 독립이 아닐 수도 있다.
- : Adam's Law
4.
⇒ 를 이용한 의 예측이 실제 에서 얼마나 빗나 갔는지에 에 대한 임의의 함수를 곱하면 항상 0. 1. 잔차(residual): 의 예측이 실제 에서 얼마나 빗나 갔는지 ⇒ 2. 가 에 대한 임의의 함수와 비상관이라는 것을 의미한다. 실제로 둘의 공분산을 구해보면 0이다.
4.1 Proof
1번 특성에 의해
Adam's Law를 적용하면 그 값은 0이 된다.
4.1.1 선형 대수학 관점에서
벡터공간에 대한 공리를 만족한다면, 이는 벡터로 다룰 수 있다. 함수, 즉 확률 변수 역시 마찬가지다. 가 만약 Multivariate Distribution이였다면 더욱 합리적이다.
조건부 기대는 를 정의역으로 가지는 함수의 집합:평면에 대한 Orthogonal Projection과 동일하다.
다시 말하면, 그 평면을 라고 하면 행렬은 에 대한 함수는 벡터 함수이므로, 그 벡터 함수들을 모아놓은 행렬과 동일하다. ⇒ 들의 집합.
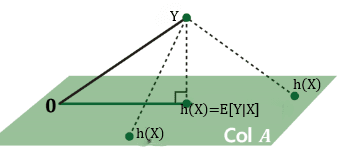
이 때, 가 에 대한 함수이므로 위에 있을 것이고, 와의 오차(MSE)를 가장 작게 하려면 의 에 대한 정사영이 되어야 한다. Least Squares와 동일한 문제이다.
는 평면 에서 까지 올라가는 벡터가 되고, 이는 와 수직이다.
는 내적()을 의미하고, 는 위의 벡터이므로 가 성립한다.
5. EVE's Law
Poisson Distribution에 대한 조건부 기대값
iid한 푸아송 확률 변수 , 가 있다고 하면
에 대해
- Linearity에 의해
- 와 는 서로 독립이므로
에 대해
1. 라고 하면
일 때, 이고 와 는 독립이므로
⇒ 이는 로 봤을 때의 Binomial Distribution의 PMF와 동일하다. 이 때, 이항 분포의 기대값은 .
2. 대칭성으로
와 가 독립적이고 동일 분포이므로,
이 때, 선형성에 의해