Two sample t-test
# Tag:
toc test
이표본 t-검정(Two sample t-test)
모집단의 분산이나 표준편차를 알지 못할 때 모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법.
기본 가정: 표본이 추출된 모집단은 정규 분포를 따라야 한다
- 귀무가설 (): 평균 간에 유의미한 차이가 없다.
- 대립가설 (): 평균 간에 유의미한 차이가 있다.
검정 통계량
과 는 표본 평균, 과 는 표본 표준 편차, 과 는 표본 크기
표본 평균 사이의 차이 를 표준 오차 로 나눈 것이 된다.
기각역(Critical Region)
t-value가 커지면, 표준 정규분포에 가까워지면서 평균차이가 있을 가능성이 커져 기각역이 늘어나게 된다.
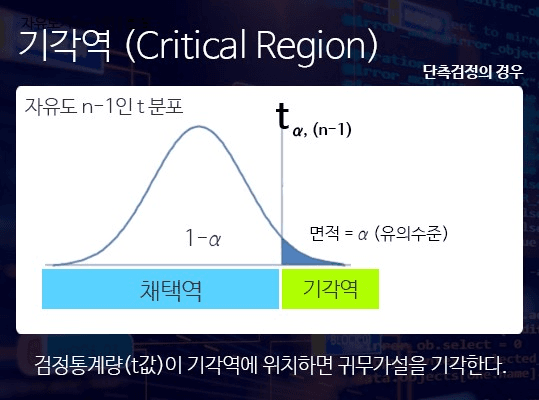
- 단측 검정: 이 때, 확률 전체의 값 에 대하여, 기각역에 해당하는 부분의 면적은 확률면적: *유의수준()*가 된다.
- 양측 검정: 양측에 대해 모두 기각역이 생긴다. 각각의 유의수준은 가 된다.
검정 규칙
p-value(유의 확률)가 선택한 유의수준()보다 작으면 귀무가설을 reject.
: 평균 간에 유의미한 차이가 있다.p-value: 귀무가설이 옳다고 가정했을 때, 통계치가 관측될 확률. 1 type error 를 범할 확률을 나타내는 것으로, 을 부정하는 것이 아니다.
보다 p-value가 작다면, 예외적인 경우가 발생하는 경우는 거의 없으며 , 그러한 사건이 발생하더라도 유의() 했기 때문으로 해석한다.
특징
- 독립된 두 집단의 평균 차이가 있는지를 검사하는 방법이다.
- 이하의 비교적 적은 수의 표본에 대해 활용. 이면정규분포와 비슷해지기 때문에 t분포 대신 정규분포를 사용해도 괜찮다.
- 모집단의 표준편차를 알 수 없을 때 사용한다. 따라서 모집단의 표준편차 대신 표본의 표준편차 를 사용한다.