or
Expectation Maximization,
기대값 최적화

Study /

AI /

Clustering /

Create : 2024년 10월 17일 21:33Update : 2025년 8월 22일 23:31

# Tag:

Source/KU_ML

EM(Expectation Maximization)

Semi-Parametric Methods의 일종으로, 숨겨져 있는 Latent variable을 가정하고, 그에 대한 최적의 기댓값을 최대화 하는 과정.

Semi-Parametric Methods는, 어떠한 확률 분포를 안다고 가정하고, 그에 대한 Random Variable인 Latent(hidden) Variable를 찾아가는 방법이다.

Parametric Methods처럼 확률 분포를 아는 것도 아니고, 그에 대한 Latent Variable(즉, parameter)도 모른다면 확률 분포를 가정하여서 Parameter를 찾아나가는 과정이다.

Random하게 만들어진 initial Latent Variable이라도, 가정한 확률 분포에 대해 Likelihood를 높여나가는 것을 반복하면 최적의 Latent Variable을 찾을 수 있음에 대한 이론을 바탕으로 만들어진 Method이다.

EM은, latent varaible $z$ 에 대해, $P (x) = z \sum P (x, z) = z \sum P (x ∣ z) P (z)$ 라는 Mixture Model을 가정하고, Likelihood에 대한 기댓값을 최대화하면서 추정해나가는 과정이 된다.
추정 과정은 Train Data를 이용해 이루어진다.

Problem when Using MLE

P (D ∣ θ) = t \prod P (x^{t} ∣ θ) = t \prod z^{t} \sum P (x^{t}, z^{t} ∣ θ) = t \prod z^{t} \sum P (x^{t} ∣ z^{t}, θ) P (z^{t} ∣ θ)

위의 Likelihood에 대해서, MLE를 거치면,

ar g θ max P (D ∣ θ) = ar g θ max t \sum lo g z^{t} \sum P (x^{t} ∣ z^{t}, θ) P (z^{t} ∣ θ)

Distribution을 알 수 없으므로, 이에 대해 여러 분포가 섞인 것으로 가정한다면, 복잡한 형태의 분포가 나타나게 된다.

$z$ : latent varaible
$θ$ : paramater, 확률 분포 $P$ 에 대한 parameter가 된다.

만약 $P (x^{t} ∣ z^{t}, θ)$ 가 지수 함수 등의 꼴로 나타난다면, 이에 대한 Sum이므로 편미분을 통해 Convex optimzation이 불가능한 문제가 나타난다.
이외에도 Mixture 모델 등이 가정 되었다면, 보통 편미분을 해서 해결 불가능한 꼴인 경우가 많다.

solution

이를 해결하기 위해 Log likelihood의 Expectation을 이용한다.

Q (θ^{'} ∣ θ) \equiv E_{z} [lo g P (D, Z ∣ θ^{'}) ∣ D, θ]

: Baum's Q-function. Log Likelihood의 **Auxiliary funciton(보조함수)**가 된다.

즉, $\hat{θ} = ar g max_{θ^{'}} Q (θ^{'} ∣ θ)$ : Expectation을 Maximization하는 방법을 변환하여 Likelihood를 최대화 시킨다.
**최적의 $\hat{θ}$ 를 찾는 것은 $P (D ∣ \hat{θ})$ 를 최대화 시키는 것과 같다. ** 이는, $\hat{θ}$ 에서 $D$ 가 관측될 Likelihood를 최대화시키는 것이다.

Q \equiv E_{Z} [lo g P (D, Z ∣ θ^{'}) ∣ D, θ] = t \sum E_{z^{t}} [lo g P (x^{t}, z^{t} ∣ θ^{'}) ∣ x^{t}, θ] = t \sum z^{t} \sum P (z^{t} ∣ x^{t}, θ) lo g P (x^{t}, z^{t} ∣ θ^{'})

Property of Baum's Q-function

$Q (θ^{'} ∣ θ) = Z \sum P (Z ∣ D, θ) lo g P (D, Z ∣ θ^{'})$ : $D, θ$ 가 주어질 때 $Z$ 의 확률 분포 하에서의 Expectation을 의미한다. $Z$ 의 모든 경우에 대해, $Z$ 가 발생할 확률을 곱한 weighted sum이라고 할 수 있다.

If $Q (θ^{‵} ∣ θ) \leq Q (θ^{'} ∣ θ)$ , then $P (θ^{‵} ∣ θ) \leq P (θ^{'} ∣ θ)$ : Jensen's inequality에 의해 성립하게 된다.

두 번째 특성은, $θ$ 의 수렴 값을 찾기 위해 반복하는 과정에서 likelihood의 증가함을 의미한다.
이는 다음과 같이 증명 될 수 있다.

Assumption : Proof of Jensen's inequality

i \sum p_{i} lo g p_{i} \leq i \sum p_{i} lo g q_{i} for 0 \leq p_{i}, q_{i} .

라는 식에 대하여, 아래의 식이 성립한다.

i \sum p_{i} \leq i \sum q_{i}

∵ 0 \leq \frac{1}{\sum _{j} p _{j}} (i \sum p_{i} lo g q_{i} - i \sum p_{i} lo g p_{i}) = i \sum \frac{p _{i}}{\sum _{j} p _{j}} lo g \frac{q _{i}}{p _{i}} \leq lo g i \sum \frac{p _{i}}{\sum _{j} p _{j}} q_{i} = lo g \frac{\sum _{i} q _{i}}{\sum _{j} p _{j}} .

Proof

Baum's Q function는 다음과 같이 풀어진다.

Q (θ ∣ θ) \leq Q (\hat{θ} ∣ θ),

\Rightarrow E_{Z} [lo g P (D, Z ∣ θ) ∣ D, θ] \leq E_{Z} [lo g P (D, Z ∣ \hat{θ}) D, θ],

\Rightarrow Z \sum P (Z ∣ D, θ) lo g P (D, Z ∣ θ) \leq Z \sum P (Z ∣ D, θ) lo g P (D, Z ∣ \hat{θ}) .

$P (Z ∣ D, θ)$ 는 Bayes' Theorem에 의해 다음과 같아지므로 다음의 식을 대입하면

P (Z ∣ D, θ) = \frac{P ( D , Z ∣ θ )}{P ( D ∣ θ )}

\Rightarrow Z \sum \frac{P ( D , Z ∣ θ )}{P ( D ∣ θ )} lo g P (D, Z ∣ θ) \leq Z \sum \frac{P ( D , Z ∣ θ )}{P ( D ∣ θ )} lo g P (D, Z ∣ \hat{θ}) .

양 변의 $P (D ∣ θ)$ 를 곱해 없애주면:

Z \sum P (D, Z ∣ θ) lo g P (D, Z ∣ θ) \leq Z \sum P (D, Z ∣ θ) lo g P (D, Z ∣ \hat{θ}) .

Jensen's Inequality에 의하여 최종적으로:

P (D ∣ θ) \leq P (D ∣ \hat{θ}) (likelihood maximization) .

E-steps

기댓값을 찾는 과정.

$θ = θ^{'}$ , $θ^{i} = θ$ 라고 가정할 때, Q function은 다음과 같아진다.

Q (θ, θ^{i}) = t \sum z^{t} \sum P (z^{t} ∣ x^{t}, θ^{i}) lo g P (x^{t}, z^{t} ∣ θ)

를 통해 기댓값을 찾는다. $θ^{i}$ 가 주어졌을 때, 새로운 $θ$ 를 사용햇을 때 Likelihood의 Expectation $Q$ 를 정의한다.

M-steps

$Q$ 를 최대화 하는 과정.

θ^{i + 1} = ar g θ max Q (θ ∣ θ^{i})

$θ$ 와 $Z$ 가 수렴할 때까지 E-step과 M-step을 반복한다. 이 과정에서, Likelihood가 상승하다가 수렴하게 되면서, Likelihood의 최댓값을 찾을 수 있다.

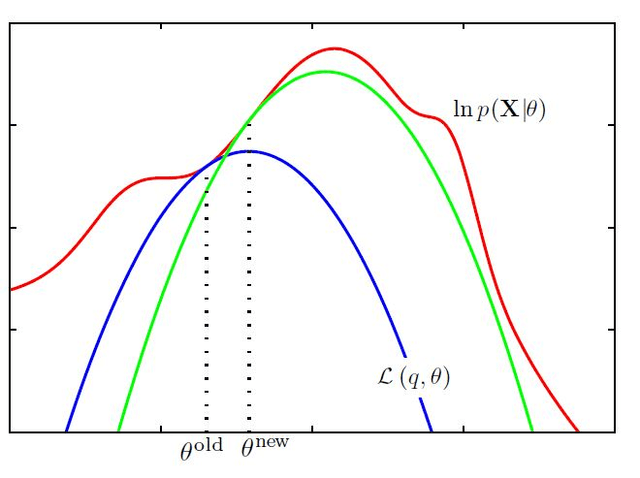
$θ^{i + 1}$ 는, 다음 E-Step의 $θ^{i}$ 가 된다.
맨 초기의 $θ^{i}$ 는, 임의의 값 혹은 다른 방법 등을 이용해 설정한다.

For MVN: (Guassian Mixture Model=GMM)

$P (x) = k = 1 \sum K N (x ∣ μ_{k}, Σ_{k}) P (g_{k})$
: $P$ 라는 확률 분포가, 여러 개의 Gaussian Distribution의 Mixture라고 본다. $k$ 는 Mixture의 개수, $P (g_{k})$ 는 해당 Guassian Mixture에 속할 확률이 된다.

$g_{k}$ : mixture component, or group, cluster. ** $k$ 번째 클러스터를 의미한다.
$P (g_{k})$ : 속할 확률이자, mixture proportion(특정 data point는 여러 개의 guassian mixture에 속할 수 있다.), mixture weight
$P (x ∣ g_{k})$ : component density, $N (x; μ, Σ_{k})$
$z^{t}$ : $x^{t} \in g_{k}$ 인지에 대한 One-hot vector, $x^{t}$ 와 일대일 매칭되는 Latent Variable이라고 할 수 있다.

이 때, 사용 되는 probablity distribution $P$ 에 대해

lo g P (D, Z ∣ θ) = t \sum lo g P (x^{t}, z^{t} ∣ θ) = t \sum [lo g P (x^{t} ∣ z^{t}, θ) + lo g P (z^{t} ∣ θ)]

$lo g P (x^{t} ∣ z^{t}, θ)$ = $lo g \prod_{k} P (x^{t} ∣ g_{k}, θ)^{z_{k}^{t}} = k \sum z_{k}^{t} lo g P (x^{t} ∣ g_{k}, θ)$
$lo g P (z^{t} ∣ θ)$ = $lo g \prod_{k} P (g_{k} ∣ θ)^{z_{k}^{t}} = k \sum z_{k}^{t} lo g P (g_{k} ∣ θ)$

정확히, $θ$ 는 ${P (g_{k}) = P (g_{k} ∣ θ^{i}), μ_{k}, Σ_{k}}$ 로 정의된다.

Q-function

$Q (θ ∣ θ^{i}) \equiv E_{Z} [t \sum lo g P (x^{t}, z^{t} ∣ θ) ∣ D, θ^{i}] = E_{Z} [t \sum k \sum z_{k}^{t} (lo g P (x^{t} ∣ g_{k}, θ)) + lo g P (g_{k} ∣ θ) ∣ D, θ^{i}]$

이 때, $Z$ 와 관련 없는 항은 Expectation에서 분리된다.

= t \sum k \sum E_{Z} [z_{k}^{t} ∣ D, θ^{i}] (lo g (P (x^{t} ∣ g_{k}, θ) + lo g P (g_{k} ∣ θ))

이 때, $E_{Z} [z_{k}^{t} ∣ D, θ^{i}]$ 는, $θ^{i}, x^{t}$ 가 주어질 때 $g_{k}$ 일 확률과 같다.
따라서 $P (g_{k} ∣ x^{t}, θ^{i}) = \frac{P ( x ^{t} ∣ g _{k} , θ ^{i} ) P ( g _{k} ∣ θ ^{i} )}{k ^ \sum P ( x ^{t} ∣ g _{\hat{k}} , θ ^{i} ) P ( g _{\hat{k}} ∣ θ ^{i} )} \equiv w_{k}^{t}$ : posterior에서 likehood $\times$ Prior로의 전환으로 볼 수 있다.

$w_{k}^{t}$ 는, label을 명백히 알 수 없으므로 어떠한 명백한 discrete 값 대신 확률로 Categoricla Distrubition과 비슷한 MLE를 진행하는 것으로도 해석 가능하다.

즉, 각 Data Point $x^{t}$ 가 어떤 확률로 $g_{k}$ 에 속할지에 대한 Posterior와 같다.

Get Parameter $θ$

$ar g θ max Q (θ ∣ θ^{i}) = ar g μ, Σ, p i max t \sum k \sum w_{k}^{t} (- \frac{1}{2} lo g ∣ Σ_{k} ∣ - \frac{1}{2} (x - μ_{k})^{⊤} Σ_{k}^{- 1} (x - μ_{k}) + lo g π_{k})$ $L \equiv w_{k}^{t} (- \frac{1}{2} lo g ∣ Σ_{k} ∣ - \frac{1}{2} (x - μ_{k})^{⊤} Σ_{k}^{- 1} (x - μ_{k}) + lo g π_{k}) - λ (k \sum π_{k} - 1)$
:와 같은, Lagrange Multiplier를 통한 Optimization 문제로 변환하자.

$\frac{d}{2} lo g 2 π$ : $ar g$ 와 관련 없으므로 생략한다.
$π = P (g_{k} ∣ θ)$ : 해당 Data들이 $g_{k}$ 에 속할 확률(예측)을 나타낸다.

first parameter: $π_{k}$

$\frac{\partial L}{\partial π _{k}} = t \sum w_{k}^{t} \frac{1}{π _{k}} - λ = 0, \frac{\partial L}{\partial λ} = - k \sum π_{k} + 1 = 0$
: $π_{k} = \frac{t \sum w _{k}^{t}}{N}$ : 위 두 조건을 연립하여 나오는 식이 된다.

second, third paramter: $μ_{k}, Σ$

$\frac{\partial L}{\partial μ _{k}} = t \sum - w_{k}^{t} \frac{1}{2} (Σ_{k}^{- 1} + Σ_{k}^{- ⊤}) (x^{t} - μ_{k}) = 0, \frac{\partial L}{\partial Σ _{k}^{- 1}} = k \sum w_{k}^{t} [Σ_{k}^{⊤} - ((x^{t} - μ_{k}) (x^{t} - μ_{k})^{⊤})^{⊤}] = 0 I$

$μ_{k} = \frac{t \sum w _{k}^{t} x ^{t}}{t \sum w _{k}^{t}}$
$Σ_{k} = \frac{t \sum w _{k}^{t} ( x ^{t} - μ _{k} ) ( x ^{t} - μ _{k} ) ^{⊤}}{t \sum w _{k}^{t}}$

이 때, $Σ_{k}$ 는 Symmetric-semi-positive-definite되므로 $∣ Σ_{k} ∣^{- 1} = ∣ Σ_{k}^{- 1} ∣$ 이 쉽게 계산될 수 있다.
Eigen decomposition을 진행했을 때, $Σ_{k} = Q Λ Q^{⊤}$ : 이 때의 $det$ 를 구하면 $= ∣ Q ∣∣ Q^{⊤} ∣Λ∣ = ∣Λ∣ = \prod_{i = 1}^{n} λ_{i}$ 이므로, 이의 역수를 구하면 바로 계산된다.