Gaussian Distribution
- or
- 가우시안 분포,
- 정규 분포,
- Normal Distribution
# Tag:
Gaussian distribution(가우시안 분포)
보통 종 모양으로 나타나게 되며, 현실 세계 현상이 자연적으로 만들어질 때의 결과가 이를 따르게 된다.
이 때, 이다.
Expectation(평균)과 Variance가 주어질 때 Entropy를 최대화하는 분포이다.
Standard Gaussian distribution
이 때, 이의 PDF는 를 따르며, 는 normalizing constant라는 상수이다. 이 모양은, 을 중심 대칭으로 하여 종 모양을 만드는 함수이다.
PDF의 정의에 따라 그 합이 1이어야 하므로,
polar coordinate로 바꾸어 풀면 (Gauss Integral)가 나오게 되고, 따라서 이다.
Standard Gaussian Distribution의 CDF는 보통 로 나타낸다.
는 대칭인 함수이므로 이 성립한다.
Mean and Variance
당연히 정의에 따라 평균은 0, 분산은 1이다.
⇒ 는 우함수, 는 기함수이므로, 적분 속의 식은 기함수이다. 이 때 부터 까지 적분하므로 0.
⇒ 따라서 분산도 1이다.
에 대해서 대칭성을 가지므로 이다. ⇒
General Gaussian distribution
- : 평균 혹은 location(center) parameter, 대칭 중심의 위치를 결정한다.
- : 표준편차 혹은 scale parameter, 분포의 퍼짐 정도와 높이 정도를 결정한다.
- 평균:
- 분산:
Standardization(표준화)
이 때, 는 dimensionless하므로, 데이터의 단위와 상관없이 비교가 가능해진다.
- CDF: 표준편차는 항상 0 이상이니, 나누어도 그 부등호 방향이 변하지 않는다.
- PDF: CDF의 미분과 동일하다. 따라서 위의 CDF를 미분하면
Property
1. 독립적인 가우시안 분포 변수들의 합 또는 차
독립적인 가우시안 분포 변수들의 합또는 차로 만들어지는 확률 변수도 가우시안 분포를 따른다.
- 평균(mean)의 경우에는 기대값의 선형성에 의해 가 된다.
- 분산(variance)의 경우에는, 두 확률 변수가 독립이므로 .
- 차의 경우에도 마찬가지 ⇒
따라서, iid인 가우시안 확률 변수 , 의 합으로 만들어지는 확률 변수 . 각각의 MGF 임을 이용해도 똑같이 증명된다.
2. 68-95-99.7 Rule(Rule of Thumb, 경험에서 근거한 법칙임)
정규 분포의 CDF 는 적분 꼴 그대로 남아 있어 컴퓨터나 표로 게산해야 하지만, 정규 분포를 따르는 값이 평균에서 특정 표준 편차 내에 있을 확률이 특정한 규칙을 따른다.
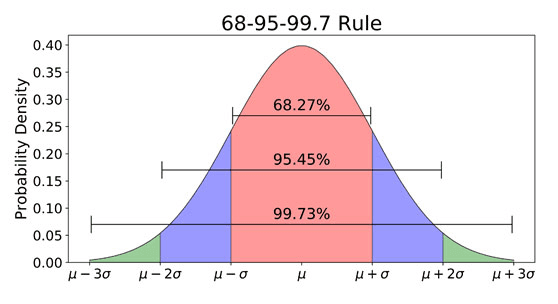
평균 로부터
- 범위 내에 가 있을 확률이 %.
- 범위 내에 가 있을 확률이 %.
- 범위 내에 가 있을 확률이 %.
Log Normal Distribution(로그 정규 분포)
에 대해서, 로그 정규 분포 는
우선 가 표준 정규 분포를 따른다고 두고, 는, 단조증가함수이므로 변수 변환을 적용 시킬 수 있다.
의 PDF 는
이에 선형 변환을 가하면 된다.