Probability

Non-naive definition of naive-Probability

모든 event가, 동일한 확률로 일어나지 않는 경우도 존재.

확률은 Bayesian에서 믿음의 정도로 보기도 하며, 어느 쪽으로 해석하든 작용하는 의미는 동일하게 된다.

확률 공간(Probability space)

S

와

P

로 구성되는 공간.

$S$ = Sample space: 어떤 event( $A$ )를 부분 집합으로 가진다.
$P$ = function, 어떤 event( $A$ )를 입력으로 하는 함수. 즉, $P$ 의 정의역은 $S$ 의 부분 집합이며, 그 출력은 0과 1사이가 된다.

두 가지 Axiom로부터 대부분의 식을 유도할 수 있으며, 확률론의 기초가 된다.

$P (ϕ) = 0, P (S) = 1$ : 공집합에 대한 확률은 0이며, 전체 집합에 대한 확률은 1이다.
$P (⋃_{n = 1}^{\infty} A_{n}) = \sum_{n = 1}^{\infty} P (A_{n})$ : $if A_{i}, A_{j} are disjoint$ : U는 합사건을 의미한다.

이로부터 유도되는 기본적인 확률의 특성은 다음과 같다.
Assumption: Let Sample Space as $Ω$ , event as $ω$ .

Complement Rule: 만약 사건 $ω$ 가 일어나지 않을 확률은 $P (ω^{c}) = 1 - P (ω)$
- $1 = P (Ω) = P (ω \cup ω^{C}) = P (ω) + P (ω^{C})$ from Axiom2 ... (1)
- $P (ω \cap ω^{C}) = \emptyset$ from Axiom 1 ... (2)
- 따라서 (1)과 (2)에 따라 성립한다.
Monotonicity(Subset Rule): 만약 사건 $A$ 가 $B$ 의 부분 집합일 경우( $A$ 가 일어났다면 $B$ 도 반드시 일어남을 의미 ⇔ $A \to B$ : 필요조건), $P (A) \leq P (B)$ 가 반드시 성립한다.
- $B = A \cup (B \cap A^{C})$ ....(1)
- $P (B) = P (A) + P (B \cap A^{C}) \geq P (A)$ from (1) : 따라서 성립한다.

두 사건

A, B

가 서로 independent하다면

P (A \cap B) = P (A) \times P (B)

가 성립한다.

independent는 한 사건이 다른 사건의 결과에 영향을 미치지 않는 것을 의미하며, 보통 동시에 일어날 수 있다. ( $\neq = disjoint$ ) $P (A \cap B)$ 는 두 사건이 동시에 일어났음을 의미한다.

Disjoint(=mutually exclusive)하다는 것은 동시에 일어날 수 없다는 것을 의미하며, 다른 한 사건이 일어났을 때, 반드시 다른 한 사건은 아예 일어날 수 없다.

벤다이어그램 상에서 겹치는 영역이 아예 없으며, 이는 indendent과 구별되어야 한다.

만약 3개의 사건 $A, B, C$ 에 대해서 각 사건이 서로 mutually independent하다면

P (A \cap B \cap C) = P (A) \times P (B) \times P (C)

가 성립한다.

단,

$P (A \cap B) = P (A) \times P (B)$
$P (A \cap C) = P (A) \times P (C)$
$P (B \cap C) = P (B) \times P (C)$ 가 모두 만족하는 것이 확인되어야 한다. 즉, 전체 독립과 쌍 독립(pairwise independence)가 모두 확인되어야 성립한다. 전체적으로 봤을 때 독립이라고 해도, 두 사건끼리는 독립적이지 않을 수 있기 때문이다.

이를 3개가 아닌 $N$ 개로 확장하더라도, $N$ 개의 사건들이 서로 완전히 상호 독립적이라면

P (A_{1} \cap A_{2} \cap \dots \cap A_{n}) = P (A_{1}) \times P (A_{2}) \times \dots \times P (A_{n})

와 동치이다.

$0 \leq P (ω) \leq 1 for every ω \in Ω$ : 모든 사건의 확률은 0 이상이고 1 이하이다. 이는 Axiom 1로부터 자명하다.
$\sum_{ω \in Ω} P (w) = 1$ or $P (Ω) = 1$ : 모든 사건의 확률의 합은 1이 된다.
$P (A \cup B) = P (A) + P (B) - P (A \cap B)$ : 두 합사건의 확률은, 각 사건 확률의 합에 곱사건의 확률을 뺀 것과 동일해진다.
- 벤 다이어그램으로 보면 다음과 같다.
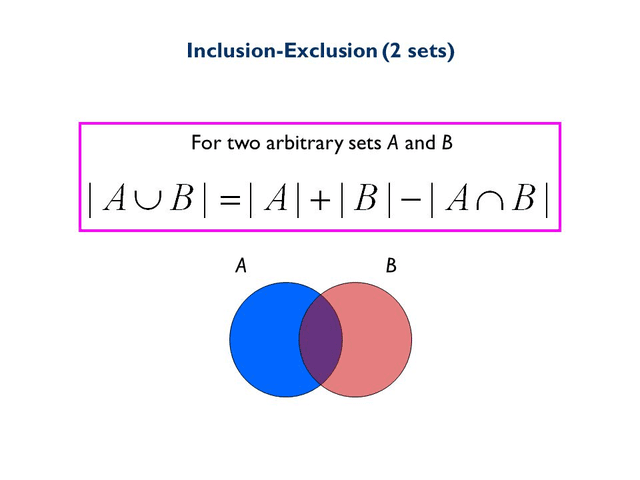
- Inclusion-exclusion Principle으로 일반화되는 원리이다.
- 만일 두 사건이 mutually exclusive라면, Disjoint(동시에 일어나지 않으므로)와 동치되므로 $P (A \cap B) = 0$ 이 된다. ⇒ Axiom 2